It's a Sign
The signs are everywhere these days.

Unfortunately, most of them are depressing and infuriating as they foretell even more depressing and infuriating times ahead. But, today is the day to focus on the positive. Sometimes signs are actually a good thing. One such example of this is with instrumental variables (IV).
In one of the earliest posts on this blog, I wrote about the finickiness of IV. In particular, I wrote about the finite sample properties of IV in exactly identified models (i.e., where the number of endogenous variables is equal to the number of instrumental variables). I talked about how while two-stage least squares estimates of over-identified models (i.e., where the number of endogenous variables exceeds the number of instrumental variables) are biased, the IV/2SLS estimator in an exactly identified model fares even worse because the finite sample moments of the estimator do not even exist.

Now, researchers typically ignore this fact and focus on the fact that IV is consistent (an asymptotic property) even in exactly identified models. Well, if your sample size is large enough (and your instrument(s) are strong), then I have no issue with you.

But, if the sample size is not particularly large, then the use of IV in exactly identified models is problematic as asymptotic properties really don't help. What can a researcher do? One option is to avoid IV. True, you can always write another difference-in-differences paper. That makes me cry.

Another option is to not have the model be exactly identified. This requires you finding additional instruments. That makes you cry.
Fortunately, there is another way.
Andrews & Armstrong (2017) provide an alternative solution. Unfortunately, it is not something of which applied researchers seem to be aware. And they should (in my opinion). Not only is the estimator useful, but Austin Nichols even provides the Cliff Notes explanation thanks to a presentation (when there were presentations) at a Stata Users Conference. [Note: I give R users permission to click the link.] Austin also provides Stata code to implement the estimator (ssc install aaniv).
What is the problem and what is the solution?
The issue is the following. In an exactly identified model, IV and 2SLS are algebraically equivalent. So, we can think about IV through the lens of 2SLS. A simple model with an outcome, y, one endogenous covariate, x, and one instrumental variable is given by
y = b0 + b1x + e
x = d0 + d1z + u,
where the equation for y is the structural equation and the equation for x is the first-stage. We can derive the reduced form for y by substituting the first-stage into the structural equation, given by
y = (b0+b1d0) + b1d1z + (e+b1u).
Assuming that z is a valid instrument, Ordinary Least Squares (OLS) produces unbiased estimates of the first-stage and the reduced form. From the first-stage, we obtain an unbiased estimate of d1. From the reduced form, we obtain an unbiased estimate of b1*d1. The IV/2SLS estimate of b1 is given by the latter divided by the former.
The IV estimator is the ratio of two unbiased estimates. Stated equivalently, the IV estimator is the product of an estimate of b1*d1 and the reciprocal of an estimate of d1. However, despite OLS providing an unbiased estimate of d1, the reciprocal of the OLS estimate is not an unbiased estimate of 1/d1. Not only is the reciprocal of the OLS estimate not unbiased, but the expectation of the ratio of the two OLS estimates does not exist.
This is the source of all the finite sample issues in IV. In fact, Hirano & Porter (2015) showed that, absent additional information from the first-stage, an unbiased estimator in the linear IV model does not exist.

But, then, along comes Andrews & Armstrong (2017). They show that by adding one -- more or less -- trivial assumption, an unbiased IV estimator is feasible! Specifically, they derive an unbiased IV estimator if the researcher knows the sign of the first-stage parameter, d1. That's it.

How often do researchers believe they have a valid instrument, but have no idea the direction of the first-stage relationship? I dare say none?
One common situation encountered by researchers where IV is used in exactly identified models and sign of the first-stage relationship is known is in a randomized control trial (RCT) with imperfect compliance. In this case, the researcher can use randomized treatment assignment to instrument for realized treatment assignment. In the absence of defiers and the presence of some compliers, the first-stage coefficient, d1, must be positive.
The estimator is detailed in the paper; or, see Austin's presentation. While Austin also does some simulations, I did my own. I used the following data-generating process (DGP) to start:
y = x + e
x = 0.5z + u
u,e ~ N2(0,0,1,1,rho)
where rho is 0.25. Setting d1 to 0.5 ensures that the instrument is sufficiently strong.
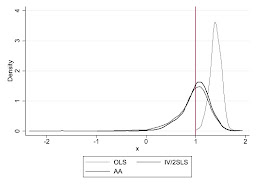
I performed 1000 repetitions for four different sample sizes, N = 50, 100, 250, and 500. Density plots of the OLS, traditional IV, and Andrews & Armstrong estimates are shown here. We see modest performance gains by Andrews & Armstrong over traditional IV when N is 50 or 100; little difference at larger sample sizes.
N=50 N=100
N=250 N=500
Then I re-did the simulations. The only thing I changed was to make the instrument weaker. Specifically, I changed the first-stage to be
x = 0.1z + u.
Now, we see more significant performance gains by Andrews & Armstrong over traditional IV even when N is 500. Aside from the increase in concentration of the estimates at the truth, we also fail to see the extremely long tails that we see with traditional IV. In fact, I truncated the density plots at +/-10, otherwise they are illegible.
N=50 N=100
N=250 N=500
It's imperative for empirical researchers to be aware of econometric advancements that can make their lives easier. Andrews & Armstrong (2017) seems to offer a definite improvement in performance when applying IV in exactly identified models in smaller samples. It also offers researchers an opportunity to display an awareness of recent econometric developments; particularly important for students looking to distinguish themselves on what will surely be a highly competitive job market for years to come.
References
Hirano, K. and J.R. Porter (2015), "Location Properties of Point Estimators in Linear Instrumental Variables and Related Models," Econometric Reviews, 34, 720-733