The Human Element

Empirical work is hard. Damn hard. Particularly when it comes to causal inference. And that's without humans getting involved. Once humans enter the fray, an insanely hard problem can become downright impossible.

The human element has led to a well-publicized replication crisis in many disciplines. Economics is not immune. A forthcoming paper by Ferraro & Shukla (2020) foretell a looming replication crisis in environmental and resource economics. The empirical practices giving rise to this forthcoming crisis are not new, nor are they unique to researchers in this field. But, they do bear repeating. And repeating. And repeating.

Ferraro & Shukla (2020) focus on a number of "questionable research practices," two of which I shall focus on here: p-hacking and multiple testing.

Let's start with p-hacking. Adam McCloskey wrote a guest blog this week on a working paper of his that I will discuss below. In it, he defines p-hacking, stating

"Broadly speaking, p-hacking refers to a researcher searching through data, model specifications and/or estimation methods to produce results that can be considered statistically significant. This behavior can take on many forms such as collecting additional data and examining multiple regression specifications."

Ferraro & Shukla (2020) offer a bit of a more tempered view, focusing instead of what they refer to as selective reporting, which they note can occur somewhat unintentionally. The authors write

"Selective reporting -- or misreporting -- of statistical significance, which often occurs in response to fears about publication bias against statistically insignificant results, can also contribute to the problem of false or exaggerated results in a literature. The opportunities for selective reporting increase as a researcher engages more frequently in the following practices: (a) analyzing multiple treatments or outcome variables; (b) using multiple identification strategies or regression specifications; (c) using multiple rules for selecting samples, trimming data, or excluding observations, or using data collection stopping rules that depend on the results obtained (e.g., 'Stop when the result is statistically significant'). Although these types of practices are often described using pejorative terms such as 'p-hacking' or 'researcher degrees of freedom,' they are not necessarily undertaken to deliberately mislead the reader. Indeed, in some cases, researchers may view them as reasonable steps to ensure the coherence and cogency of the final publication."

I think we all understand that selective reporting or p-hacking is problematic, but perhaps we may not fully appreciate why this is so. There are two interesting ways -- to me -- to think about the problem. I'm sure I'm not the first to conceptualize the issue in these two ways, but I can't explicitly recall seeing either written down.

The first is to think about the selective reporting of results as a form of pre-test bias. In a previous post on this blog, I discuss the issue of pre-test bias in a different context. This is an issue that is well known amongst time series econometricians, but rarely makes its way into the vernacular of microeconometricians (see Roth (2020) for a recent exception in the context of difference-in-differences models). 

The notion of pre-test bias dates to Bancroft (1944). The idea is simple. When we use a specification test to decide between two estimators, we are really inventing a third estimator. This third estimator can be expressed as

θ-hat(PTE) = I(Fail to Reject) * θ-hat(1) + I(Reject) * θ-hat(2)

where PTE stands for pre-test estimator, θ-hat(1) and θ-hat(2) are the two competing estimators, and I() is an indicator function. I(Reject) equals one if our specification test rejects the null hypothesis that estimator 1 is preferred; I(Fail to Reject) equals one if I(Reject) equals zero.

Bancroft points out that θ-hat(PTE) is biased. This occurs because the estimator is a weighted average of our two estimators -- where the weights will be 0 or 1 -- but the weights are themselves random variables. Recall, if we have two random variables, X and Y, then E[XY] does not generally equal E[X]E[Y]. So, even if, say, θ-hat(1) is unbiased, the estimator that chooses θ-hat(1) after a specification test is not unbiased.

Selective reporting is a form of a pre-test estimator as the final estimator is chosen on the basis of the outcome of one or more statistical tests. However, instead of the test being some usual specification test that we are familiar with (e.g., a Hausman-like test), the "test" is the p-value of different estimators. Thus, our p-hacked estimator, PHE, can be written as 

θ-hat(PHE) = I(p(1)<0.05) * θ-hat(1) + I(p(2)<0.05) * θ-hat(2) + ... ,

where p(i) is the p-value associated with the null hypothesis that θ-hat(i) = 0. The properties of PHE are not what we think they are and, hence, are unlikely to stand up to scrutiny or replication. Whenever researchers are "selecting which results and research hypotheses to present only after the results are known," they are using a PHE (Ferraro & Shukla 2020). If they do not convey this fact to readers, well ...

Evidence of widespread selective reporting is usually given by examination of the distribution of p-values across studies. A mass right below usual thresholds is an indication of manipulation, as those familiar with regression discontinuity estimators are well aware. Arpit Gupta tweeted about a working paper by Brodeur et al. (2019) that compares the distribution of test statistics by empirical method. Perhaps apropos of nothing (causation, correlation, yada yada), regression discontinuity studies display the least evidence of selective reporting. 

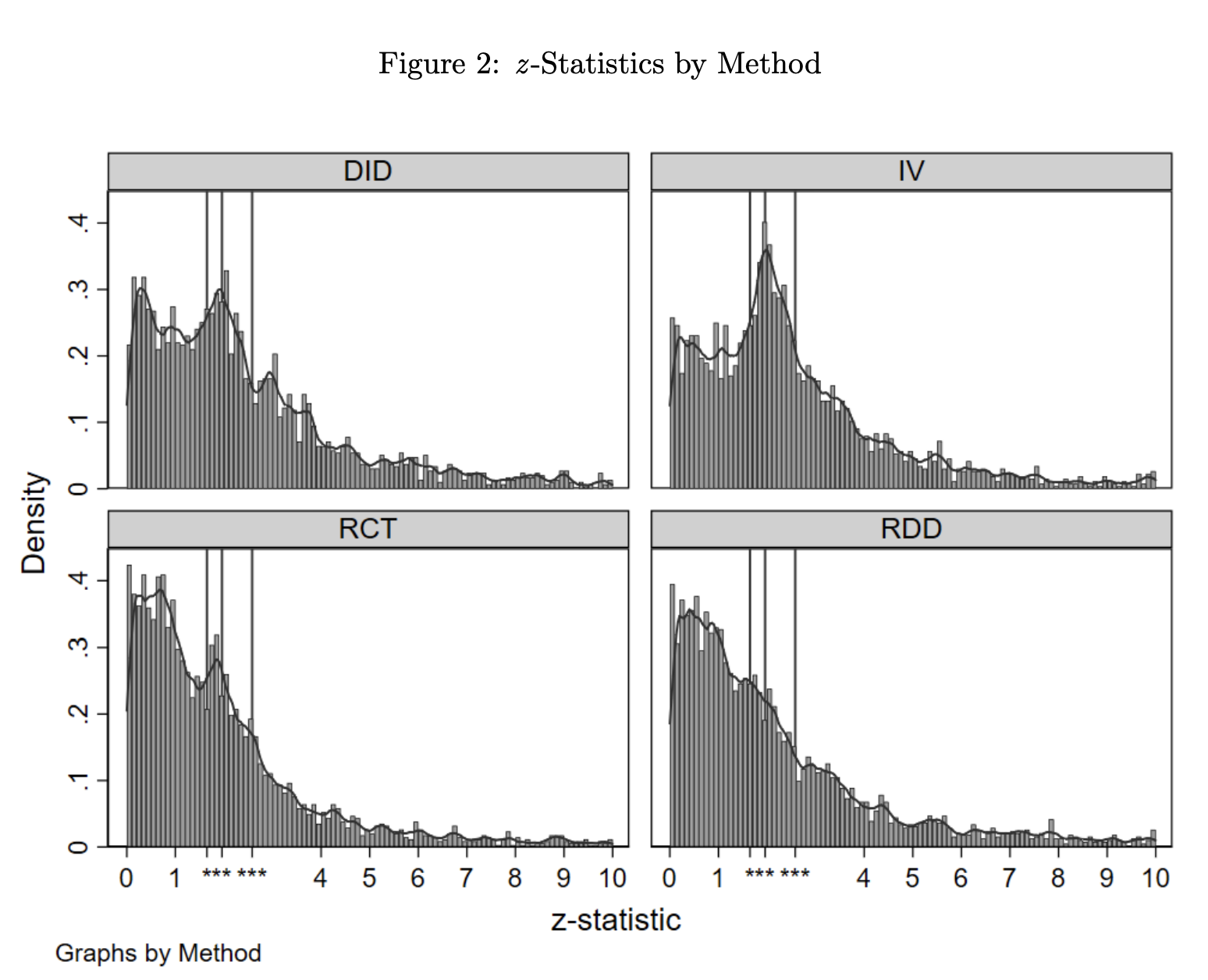
Ferraro & Shukla (2020) do not distinguish among empirical methods, but do find evidence of selective reporting overall in the environmental and resource economics studies they assemble.

The connection between p-hacking and Bancroft's pre-test bias may not be overly common, as I said, since pre-test bias is more in the domain of time series econometricians. Similarly, the other way I think about p-hacking borrows from micro theory. Specifically, the idea of the winner's curse. 

I never learned about the winner's curse in school. But, it's a simple, straightforward, and cool idea. Think about a bunch of agents (e.g., firms or individuals) bidding on an object (e.g., a contract for a project or an object such as a painting). The object has a true valuation. Each agent observes a private signal of this valuation, which is a random draw from a distribution centered on the true value. Thus, signals are unbiased. Given the signal, the agent bids on the object. 

Yes, there are lots of auction formats that people who love auctions like thinking about ...

... but what we know is that the agent receiving the highest signal will bid the most and, depending on the auction format, will likely win. This signal will come from the upper tail of the signal distribution and will be way above the true valuation of the object (if the number of bidders is large). As a result, when the agent wins the auction, they will be very unhappy in hindsight as they overpaid for the object.

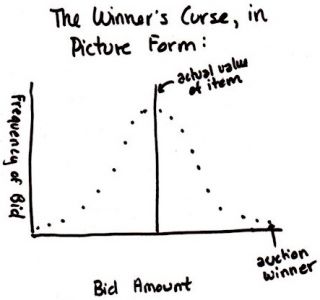
In the auction that is the allocation of scarce journal space, we are all agents bidding for a piece of the object. And, given current practices or at least beliefs about current practices, statistical significance is the currency in which we bid. In the end, the auction winners are those who receive signals far from what is expected, in the upper tail of the distribution of test statistics.

Unlike the traditional winner's curse, where the auction winner is left only with negative profits due to overpaying for the object, in the publication version of the winner's curse, the auction winner is left with a sullied reputation when their study falters under scrutiny. The retraction is the ultimate form of bankruptcy.

Other than just telling researchers to knock it off (see Andrew Baker's tweet ... I assume he doesn't have kids!), there have been some suggestions on how to curb p-hacking.  Benjamin et al. (2018) propose using a stricter threshold of p<0.005 to denote statistically significant results; all higher p-values to be described as statistically suggestive. To my knowledge, this has not become the norm. Nor does it really solve the problem, especially as data sets increase in size. The new paper I mentioned above by McCloskey & Michaillat (2020) similarly advocates for a stricter standard, but in their framework the standard is endogenous to the incentives to engage in questionable research practices. Pre-analysis plans are another way by which the profession seeks to limit selective reporting, although it is unclear how successful this will be. Anderson & Magruder (2017) propose a hybrid approach, combining pre-analysis plans with split sample strategies.

As a I wrote in a prior post, my preference is simply to move away from binary conclusions of statistical significance and instead focus on confidence intervals where the question of whether zero lies in the interval or not is given substantially less prominence in the evaluation of studies. Binary decisions will always incentivize manipulation.

In addition to selective reporting, Ferraro & Shukla (2020) also focus on the researcher practice of multiple testing. I imagine nearly everyone has seen this

Nonetheless, a reminder ... When one conducts K (independent) tests using a 5% significance level and the null is true for all tests, the probability of falsely rejecting at  least one null is (1 - 0.95^K). Two trends in empirical research have made concerns of false discoveries due to multiple testing more salient. First, more data are available, often because researchers are involved in data collection efforts. This leads to more interesting outcomes in the data and, hence, more models being estimated. Second, there is considerable interest in heterogeneous effects of treatments across observed groups. As a result, researchers are splitting their samples and estimating the same models across multiple groups. 

This all seems innocent and well-motivated. Nonetheless, it leads to the jelly bean conundrum. Take four outcomes and five sub-samples. That yields 20 estimates assuming only one specification per case. If a treatment has no effect on any outcome for any group, there is a 65% chance that the researcher obtains at least one statistically significant treatment effect estimate.

Again, there are solutions as telling researchers to knock it off is not optimal here. We want to assess effects on multiple outcomes. We want to assess heterogeneity across groups. But, we need to do it right. I am no expert on multiple testing, but the oldest and most well-known solution is the Bonferroni correction. This is trivial to do. It simply entails adjusting the threshold for statistical significance to fix the family-wise error rate, or the probability of making at least on Type I error. In my example above with 20 estimates, the Bonferroni correction simply uses a p-value of 0.05/20 = 0.0025 as the cutoff when deciding whether to reject each of the 20 nulls (as 1 - 0.9975^20 = 0.95).  Other corrections exist as well.

Yes, Brain, I'll try to help the humans be better.

Update (7.6.20)

Check out David McKenzie's blog on multiple testing in Stata.

At least a few papers that have made the connection to the winner's curse. See, e.g., Young et al. (2008). Andrews et al. (2019) address correcting inference to avoid the curse.

Elliott et al. (2020) discuss testing for p-hacking by moving beyond examination of the distribution of p-values across studies.

References

Anderson, M.L. and J. Magruder (2017), "Split-Sample Strategies for Avoiding False Discoveries," 

NBER Working Paper No. 23544

Andrews, I., T. Kitigawa, and A. McCloskey (2019), "Inference on Winners," unpublished manuscript

Bancroft, T.A. (1944), "On Biases in Estimation Due to the Use of Preliminary Tests of Significance," Annals of Mathematical Statistics, 15(2), 190-204

Benjamin, D.J., et al. (2018), "Redefine Statistical Significance," Nature Human Behavior, 2, 6-10

Brodeur, A., N. Cook, and A. Heyes (2019), "Methods Matter: P-Hacking and Causal Inference in Economics and Finance," unpublished manuscript

Elliott, G., N. Kudrin, and K. Wüthrich (2020), "Detecting p-hacking," unpublished manuscript

Ferraro, P.J. and P. Shukla (2020), "Feature - Is a Replicability Crisis on the Horizon for Environmental and Resource Economics?" Review of Environmental Economics and Policy, forthcoming.

McCloskey, A. and P. Michaillat (2020), "Incentive-Compatible Critical Values," unpublished manuscript

Roth, J. (2020), "Pre-test with Caution: Event-study Estimates After Testing for Parallel Trends," unpublished manuscript

Young, N.S., J.P.A. Ioannidis, and O. Al-Ubaydli (2008), "Why Current Publication Practices May Distort Science," PLOS Medicine, 5(10): e201. https://doi.org/10.1371/journal.pmed.0050201