IV with a Mismeasured Binary Covariate

The issue here is to consider a very simple model,

Y = a + b*D + e,

where D is a binary variable and b is the coeff of interest. Suppose D is endogenous, but we have a valid instrument, z. IV is consistent and should do well in large samples if z is strong.

 But what if D is also measured with error? I.e., what if the true model is

Y = a + bD* + e,

where D* is the true D, but we only observe D (D not equal D* for some i)? That valid instrument, z, we had? Now, it's not quite as useful. Why?

 Because ME in a binary var canNOT be classical. When D*=0, the ME can only be 0 or 1. When D*=1, the ME can only be 0 or -1. Thus, the ME is necessary neg. corr. with D*. Since the IV, z, is correlated with D*, it is almost assuredly also correlated with the ME and thus invalid.

 A very good reference is Black et al. (2000). Note, this argument applies to any bounded variable; D* need not be binary. E.g., if D* represents a percentage, then it is bounded on the unit interval. If the bounds are relevant, same issue arises.

 So, is this a big deal? Most applied people would answer a question about this: "ME is not a big deal in this context. If it is exists, it's not severe enough to matter." Perhaps. Perhaps not. I performed some simulations.

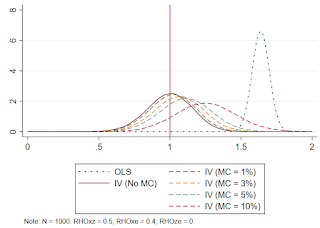
 The first simulations are based on 250,000 reps with N=1000 and a strong IV. I consider random ME in 1%, 3%, 5%, and 10% of each sample. The IV estimates are biased toward OLS, and one could argue at least moderately so with 5% misclassification.


In an old paper of mine, I cite several instances where 10+% misclassifcation has been documented in commonly analyzed treatments (e.g., training, education, union status around 5%.

 Not surprisingly, if the IV is weak, then results are even worse.

So, what do we do? There are a few solutions out there, many that rely on computing bounds. But, definitely an important area for future work! One very recent contribution to this literature is by my great friend, Rusty Tchernis and co-authors.

Note: Code is available here: http://faculty.smu.edu/millimet/blog.html

 References
Black, D.A., M.C. Berger, and F.A. Scott (2000) "Bounding Parameter Estimates with Nonclassical Measurement Error," Journal of the American Statistical Association, 95, 451, 739-748

 Nguimkeu, P., A. Denteh, and R. Tchernis (2019), "On the Estimation of Treatment Effects with Endogenous Misreporting," Journal of Econometrics, 208, 2, 487-506

Popular posts from this blog

The Great Divide

Image
I applaud the fact that the American Economic Association, the European Economic Association, the Econometric Society, and the Royal Economic Society have established an ad-hoc joint committee tasked with proposing ways to improve the publication process in economics. I encourage everyone to fill out the survey  (limited to members of the AEA, EEA, ES, and RES, however) even though I am quite cynical about what may come of it. Although only tangentially related, I decided to write a post about a topic that vexes me (and others to whom I have spoken, but I will leave it to them to out themselves) at the intersection of the Venn diagram containing publishing (editing and refereeing), teaching, and econometrics.   What lies at this intersection is the great divide between theoretical and applied econometrics, both in the classroom and in the wild.  As I have progressed in my career, I have enjoyed writing more econometrics papers and fewer economics papers per ...
Read more

There is Exogeneity, and Then There is Strict Exogeneity

Image
Panel data has become quite abundant. As a result, fixed effects models have become prevalent in applied research. But, this week I handled a paper at one of the journals for which I am on the editorial board and was reminded of a mistake that I have seen all too frequently over the years. Most researchers are probably aware of the issue I am highlighting, but indulge me. In a cross-sectional regression model, we have y_i = a + b*x_i + e_i OLS is unbiased if x is exogenous , which requires that Cov(x_i,e_i) = 0. In other words, the covariates need to be uncorrelated with the error term from the same time period. In contrast, in a panel regression model with individual effects, we have y_it = a_i + b*x_it + e_it If we wish to allow for the possibility that Cov(a_i,x_it) differs from zero, then a_i is a "fixed" effect instead of a "random" effect. To understand what we need to assume to obtain unbiased estimates of b, we need to understand how the model i...
Read more

Black Magic

Image
The world is a very different place from when I started this blog. The pandemic is over ... but I'm not sure we are in a better place. Different, not necessarily better. This brave new world has made it hard for me to find the time and mental energy to continue this blog. Moreover, with the changes at #EconTwitter ( X ) , no one may read this anyway. Nonetheless, I move forward and we shall see if this post (and any future posts) provide utility to anyone beyond myself.  So, I have spent some time thus far this summer revising my lecture notes (available here  ... although it is still in progress for some). I still stand firm in my belief that all empirical researchers ought to teach econometrics (if for no other reason as a constant reminder that there is more to the field than diff-in-diff). As I did so, I added two new extensions to my discussion of -- what else -- measurement error. But, this post is not about measurement error per se. Really. No, I mean it. Instead, it is...
Read more