Wait for It

While certain individuals on #EconTwitter have gotten me hooked on an undisclosed Netflix show that my teenage daughter loves and my teenage son makes fun of me for watching, my kids and I all agree on one truly fantastic show:

The main characters are Shawn and Gus. Shawn helps the Santa Barbara police department solve crimes given his unique skill. He is hyper-observant. His skill was developed during childhood by his father, a police detective. However, Shawn convinces the police department he is psychic. Together, Shawn and Gus, best friends since childhood, run Psych, a psychic detective agency.

As a result of Shawn's psychic-ness, he often "sees" the future and helps the police nab the criminal. One of Shawn's catch phrases in the show is "Waaaaaaiiiiiittttt for it!".

Seeing the future and waiting for it aren't just common themes in Psych. They are also common themes -- either explicitly or implicitly -- in econometrics. Specifically, continuing on the topic from my previous post, these are common themes in difference-in-differences (DID) and synthetic control methods (SCM). 

Seeing the future relates to the well-known parallel trends assumption required for DID analysis to yield an unbiased estimate of the average treatment effect on the treated (ATT). Similarly, seeing the future relates to the assumption required for SCM that the treatment unit and the synthetic control would have evolved in lockstep.

Let's focus on DID. In the standard 2x2 DID design, the researcher has two periods of data, t = 0,1. No units are treated in the initial period. In the terminal period, some units have received the treatment. The treatment group is denoted by D = 1, the control group by D = 0. The parameter of interest, the ATT, is given by the difference between the observed mean outcome of the treatment units in period 1 minus the expected outcome of the treatment units in period 1 in the absence of treatment. Since the treatment units are all treated in period 1, this expected outcome is the missing counterfactual.  It is only visible if we know how to cross over to a parallel universe.

Absent this ability, the DID approach estimates this missing counterfactual by assessing how the average realized outcome changes over time for the control units and assumes the average outcome for the treatment units would have evolved in parallel. This allows one to estimate the counterfactual expected value for the treatment units in period 1 by simply adding this change to the average outcome for the treatment units in period 0. The ATT then follows as the difference between the average realized outcome for the treatment units in period 1 and this counterfactual expected value. 

Denoting the outcomes with and without the treatment as Y(1) and Y(0), respectively, the DID estimator can be visualized like this:

Now, this is all straightforward if you have had any exposure to causal inference. But, what I think is a little bit less straightforward and less appreciated is the testing of the parallel trends assumption in applied research. Because DID is entirely dependent on this assumption, it would certainly be wonderful if we could test it. To that end, researchers typically do two related things if more than one year of pre-treatment data is available.

Suppose data are available on all units in periods -1, -2, and so on, where all units remain untreated in these time periods preceding period 1. First, graphs of the type shown above can be extended further back in time to see if the average outcomes of the treatment and control units evolve in parallel fashion across these pre-treatment periods. Second, this can be formally assessed by estimating what is referred to as an event study model. The event study model allows for the treatment to have a time period-specific effect in every pre-treatment (and post-treatment) period.  This can then visualized like this:

   

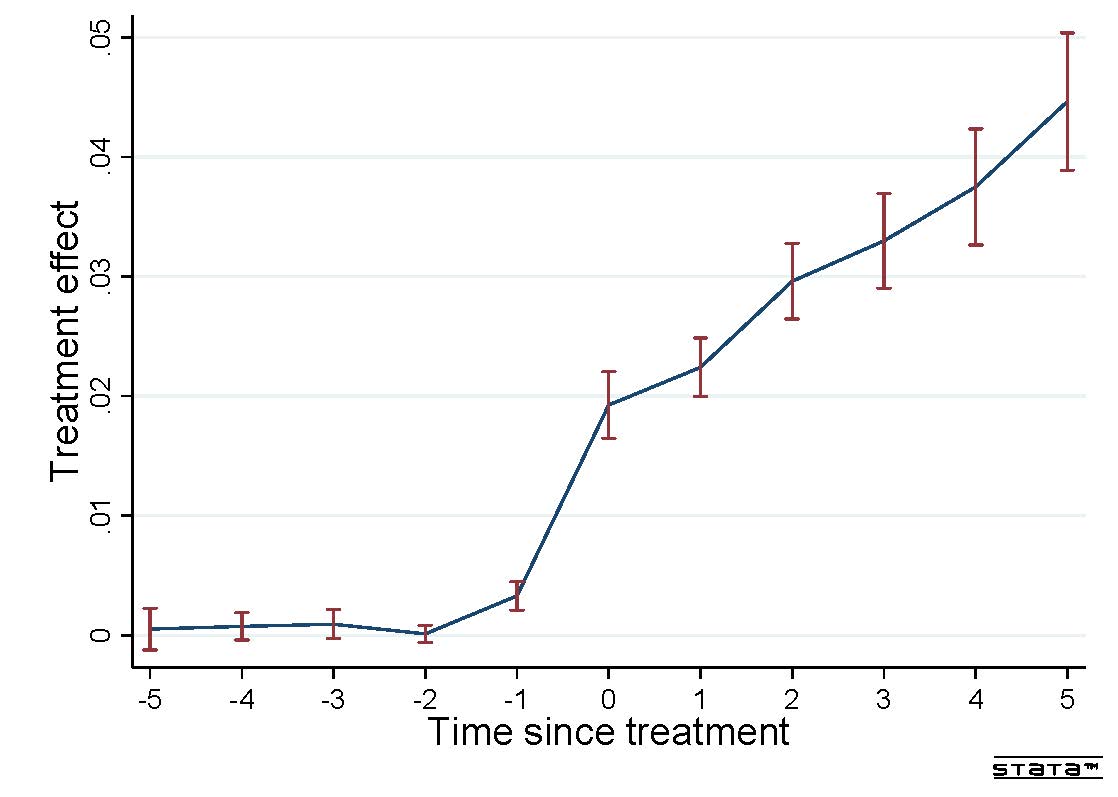
In both cases, a lack of divergence in the trends in the outcome across the treatment and control units in the pre-treatment periods is often taken as a test of the parallel trends assumption. 

While many assuredly know, it is crucial that researchers and consumers of research are aware that these procedures are not a test of the parallel trends assumption. At best, they provide suggestive evidence that the assumption holds. As stated above, the parallel trends assumption relates only to whether outcomes would have evolved in parallel between periods 0 and 1. And, since we are not Shawn -- we are not psychic and able to "see" into the future -- this can never be known. 

The parallel trends assumptions is fundamentally untestable.  

At this point, you might be thinking that, while technically correct, nice event study graphics like those above are soooo convincing that this is just semantics. Perhaps, perhaps not.

To start, we need to return to the 1970s. Fortunately, Shawn and Gus are there waiting for us (in episode 5 of season 3, entitled "Disco Didn't Die. It was Murdered!").

In Ashenfelter (1978), he noted that treatment units in a job training program suffered a negative earnings shock prior to treatment. Ashenfelter writes (p. 51): [T]he earnings of trainees tend to fall, both absolutely and relative to the comparison group, in the year prior to training." This adverse shock in the pre-treatment period that induces some units to self-select into treatment subsequently became known as Ashenfelter's Dip. Since the dip is a time-varying shock differentially affecting the treatment and control units, it invalidates the parallel trends assumption. 

But, wait, you say! This is exactly what the event study model is designed to detect. If there is a dip, it will be evident in graphics like the one above. Again, perhaps, perhaps not. This is where the second part of Psych comes into play. Wait for it.

In DID setups, it is obviously critical to know when the treatment occurs. In the notation above, the treatment units receive the treatment between periods 0 and 1. However, in many applications, pinning down the precise time of the intervention may not be obvious. This arises because, while the researcher cannot "see" the future, agents might. And, armed with knowledge of what is to come, they may adjust their behavior now. In other words, they may not wait for it.

For example, if the treatment is a policy change such as enacting a free trade agreement, raising the minimum wage, or altering the health care system, agents certainly know what is coming down the pipeline before it arrives. Even individual-level treatments, such as changes in health insurance coverage or layoffs, may be known before they actually occur.

When agents know what is coming, we as economists would expect them to adjust their behavior immediately, rather than waiting for it. This leads to anticipatory effects of the treatment. 

Estimating anticipatory (and lagged) effects of a treatment is the subject of a wonderful paper that does not get its due (in my opinion). LaPorte & Windmeijer (2005) consider a standard two-way fixed effect (TWFE) panel data model with an individual-level treatment, marital status. In particular, they estimate a model including only married individuals in the initial period and the treatment is getting a divorce. The outcome is a measure of mental well-being. They find, not surprisingly, that mental well-being falls before a divorce becomes official, presumably due to the stress and emotional toll of the process itself, and then gradually increases post-divorce.  

Many treatments may induce such anticipatory effects. For example, if firms know that the minimum wage will increase next year, they may adjust the capital-labor mix this year. If firms know that a free trade agreement will reduce tariffs next year, they may change their overseas suppliers this year. If individuals know they will experience a change in health insurance coverage next year, they may adjust their risk-taking today.

The point concerns "testing" the parallel trends assumption with an event study model. In the presence of both an Ashenfelter-type dip and anticipatory effects of the treatment, it is quite possible that these will offset and the event study graphic will provide suggestive evidence that the parallel trends assumption holds, when the truth is it does not. 

For example, suppose that two countries experience a simultaneous reduction in political ties and bilateral trade. In an effort to repair their political ties, the countries form a free trade agreement. The data may show no evidence of any pre-treatment differences between the treatment and control units due to the offsetting Ashenfelter-type dip in bilateral trade and the anticipatory effects of the forthcoming trade agreement. 

Or, suppose that there is a relative decline in automation by firms located in a particular state. The state may then decide now is a good time to raise the minimum wage. The higher minimum wage is announced for the following year. Again, data may show no evidence of any pre-treatment differences between the treatment and control units due to the offsetting Ashenfelter-type dip in automation and the anticipatory effects of the forthcoming minimum wage hike. 

In both of these examples, a quiet event study may mask a lot of action beneath the surface. 

Action that invalidates the parallel trends assumption.

As a final comment, note that these same issues apply to the SCM as well. In SCM, the timing of the treatment is also crucial since the weights for the synthetic control are fit from the data in the pre-treatment period. If there is an Ashenfelter-type dip, the synthetic control should fit this dip as well. However, if there are anticipatory effects of the treatment, the synthetic control should not fit these effects or else some of the treatment effect is likely to be masked. 

Abadie et al. (2010, p. 494) state this explicitly: "In practice, interventions may have an impact prior to their implementation (e.g., via anticipation effects). In those cases, T0 could be redefined to be the first period in which the outcome may possibly react to the intervention." However, this might not be possible if an Ashenfelter-type dip and anticipatory effects occur over the same time period.

At the end of it all, we are not psychic. We cannot travel to parallel universes. Thus, the parallel trends assumption is not testable. Consequently, it is imperative that researchers, first, do not treat it as testable (by describing assessments of pre-trends as such) and, second, think carefully about timing and the reasons for selection into treatment. Researchers then need to rely on this institutional knowledge, in addition to event study models, for DID estimates to be persuasive. It won't be easy, but ...

Coincidentally, Andrew Goodman-Bacon tweeted the following this week:

"There are a million ways to trust DD too much and a million ways to write it off too quickly."

My objective here is not to add to either ledger. Perhaps a simultaneous occurrence of an Ashenfelter-type dip and an offsetting anticipatory effect of treatment is highly unlikely. 

 

Rather, my objective is simply to implore researchers not to forget the fundamental problem of causal inference (Holland 1986). This refers to the fact that the counterfactual is missing and can never be observed, except by the likes of psychics, such as Shawn, or those who can move between parallel realities, such as Elaine.

The rest of us can only venture a guess. As such, any estimate of the missing counterfactual is ultimately a guess -- albeit hopefully an educated one -- that must rely on at least some assumptions that are not testable. The parallel trends assumption is the untestable assumption in DID and SCM. So, whether DID is to be trusted in a particular application, well

UPDATE (5.23.2020)

Malani & Reif (2015) have an excellent paper, with an application, on the importance of anticipation in the interpretation of pre-trends, along with an application to tort reform. 

Roth (2020) looks like an excellent paper that will surely be critical to this literature. He writes:

"This paper provides theoretical and empirical evidence on the limitations of pre-trends testing. From a theoretical perspective, I analyze the distribution of conventional estimates and confidence intervals (CIs) after surviving a test for pre-trends. In non-pathological cases, bias and coverage rates of conventional estimates and CIs can be worse conditional on passing the pre-test."

References

Abadie, A., A. Diamond, and J. Hainmueller (2010), “Synthetic Control Methods for Comparative Case Studies: Estimating the Effect of California’s Tobacco Control Program,” Journal of the American Statistical Association, 105, 493-505 

Ashenfelter, O. (1978), "Estimating the Effect of Training Programs on Earnings," Review of Economics and Statistics, 60(1), 47-57 

Holland, P. (1986), "Statistics and Causal Influence," Journal of the American Statistical Association, 81, 945-960

Laporte, A. and F. Windmeijer (2005), "Estimation of Panel Data Models with Binary Indicators When Treatment Effects are Not Constant Over Time," Economics Letters, 88(3), 389-396

Malani, A. and J. Reif (2015), "Interpreting Pre-trends as Anticipation: Impact on Estimated Treatment Effects from Tort Reform," Journal of Public Economics, 124, 1-17

Roth, J. (2020), "Pre-test with Caution: Event-study Estimates After Testing for Parallel Trends," unpublished manuscript.