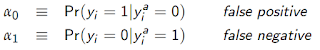Don't Reinvent the Wheel
Do you ever feel like you are racing and racing and racing, trying to find new research ideas or figure out how to answer an existing research question, but never making any progress? [No, I'm not specifically looking at you!]

An often fruitful way to come up with new research questions, or new ways to answer existing research questions, is to borrow approaches that were designed for completely different purposes. I will give you two examples that illustrate this idea and that I find super interesting ... because both have something to do with measurement error.

But, this post is really not about measurement error. Trust me.
I wrote about the first example in a previous post here for an entirely different reason. To review, Hausman et al. (1998) propose a solution to misclassification of a binary outcome in a logit (or probit) model. To understand their approach, assume that a logit is the correct model if the true (actual) outcome, y^a, is observed. However, the rates of false positives and negatives are given by
The authors then derive the probabilities for the observed outcome, y, given by
All of the parameters can be estimated via Maximum Likelihood using these probabilities. As discussed in the previous post, the model is identified because of the non-linearity of the logit probabilities.
Now, this is clearly a model about measurement error. As such, you would likely only know of this paper if (i) you did a google search on misclassification in binary choice models, or (ii) you were forced to have me (or someone similarly like-minded and forward-thinking) as your econometrics professor.

But, what is this model really about? The framework here -- at its core -- contains a binary outcome, y^a, that depends on the covariates, x. However, the binary outcome being observed in the data, y, may differ. That's it. In Hausman et al. (1998) this divergence happens because of misclassification. But measurement error does not have to be the only reason for this divergence!

One can re-cast or re-interpret the model and analyze divergences between y and y^a that arise for any reason. For example, another reason for divergence between y and y^a might be because agents make sub-optimal decisions. In other words, if the outcome captures a binary choice made by agents and x reflects determinants of this choice, then y^a can be re-interpreted not as the true value of the outcome, but rather the optimal choice of the agent.
Consider a random utility model, where an agent's utility is given by
U(0) = x*b0 + e0
U(1) = x*b1 + e1
where U() is the agent's utility from choosing zero or one and the errors are distributed as Type I extreme value. With this structure, the probability that the agent's utility is higher under each option is given by the logit probabilities above. Specifically,
Pr(y^a = 1) = exp(xb1)/[1+exp(xb1)],
where b0 is normalized to zero. Thus, the logit estimates allow us to learn the effects of the covariates on the relative utilities of the two choices.
But, what if agents are fallible?

If at least some agents make sub-optimal choices, then the observed choice, y, will diverge from the optimal choice, y^a. In this case, the Hausman et al. (1998) model can be used to (i) obtain consistent estimates of the parameters in the presence of these sub-optimal choices, and (ii) estimate the percentage and types of sub-optimal decisions being made. The model is applicable despite this application having nothing to do with measurement error.

By re-interpreting what y, y^a, a false positive, and a false negative capture, we are able to take an existing model and use it for a completely different purpose and to answer a completely different research question. In fact, this was done in Palangkaraya et al. (2011). Here, the authors are interested the decision by patent offices to approve or reject a patent application. The outcome y^a is interpreted as the "correct" decision. The observed outcome, y, will deviate if the patent office makes the wrong decision. Using the Hausman et al. (1998) model, the paper practically writes itself.
One can think of tons of other potential applications of this approach. I say potential as one still needs to justify the implicit assumptions of the model. Nonetheless, applications might include approval decisions of loan applications or applications for public safety net programs such as unemployment insurance or disability benefits, voting decisions by policymakers, judicial decisions, etc.

A second example of taking a model designed for one problem and re-casting it solve a completely different problem comes from a recent paper I wrote with Chris Parmeter. To start, let us review what is known as a stochastic frontier model (SFM). The SFM was developed in Aigner et al. (1977) and Meeusen & van den Broeck (1977). The objective is to explain the inefficiency of firms; the fact that not all firms appear to be producing on the production frontier.

In the graph, two firms -- one using Xa and one using Xb amount of inputs -- are observed to be producing well below the production frontier, at points A and B, respectively. How can this be? An early explanation for this was measurement error. But, that was deemed to be an unsatisfactory explanation.

Then, the idea that firms may be inefficient was proposed. But, how to estimate an empirical model to allow for this? Enter the SFM.
The model begins by allowing for the production function to be stochastic rather than deterministic. A firm's maximum possible output, y*, as a function of inputs, x, is assumed to be given by
y* = f(x,b) + v
where v represents random, statistical noise. If the firm is fully efficient, then y equals y*. If the firm is inefficient, then y will be strictly less than y*. Hence, y must be less than or equal to y* and is expressed as
y = y* - u
where u ≥ 0. Combining these two equations, one is left with a model for observed output given by
y = f(x,b) + e,
where e = v - u.
The SFM model makes parametric distributional assumptions on v and u (e.g., normal and half-normal, respectively) along with a functional form assumption for the production function, f(), and then estimates b via maximum likelihood. After estimation, the residuals, e-hat, can be decomposed into v-hat and u-hat as derived in Battese & Coelli (1988). Thus, the estimation procedure produces not only estimates of the production function, but also observation-specific estimates of inefficiency.

Now, the SFM was clearly developed with a single purpose in mind. As such, you would likely only know of this model if (i) you were interested in efficiency analysis, or, again, (ii) you were forced to have me as your econometrics professor.
But, as in the previous example, what is this model really about? The framework here posits a regression model with a continuous outcome, exogenous covariates, and a negatively skewed error term arising from a two-sided and a one-sided component. In the SFM, the one-sided error component is attributed to inefficiency. But inefficiency does not have to be the only reason for this one-sided error component!
By re-interpreting what y, y*, and u capture, we are -- once again -- able to take an existing model and use it for a completely different purpose and to answer a completely different research question. In my paper with Chris, we show how the SFM can be used to address ... wait for it ... measurement error in the dependent variable of a regression model.

If you spent any time learning about measurement error, you might vaguely remember that measurement error in a continuous dependent variable is not particularly problematic; a little efficiency loss, but no bias. But, this assumes the measurement error is classical, and one requirement for classical measurement error is two-sided-ness. In many situations, however, we may think the measurement error might be one-sided. For example, when the outcome is self-reported and concerns something with a stigma attached (e.g., drug use, criminal behavior, or pollution as I discussed in a previous post here). Or, data may contain one-sided measurement error because the data miss relevant instances of the phenomenon being measured (e.g., crime statistics, causalities in conflicts or wars, or COVID-19 cases or deaths). In these situations, then one might think that observed, y, is no greater than y* and hence, u, represents one-sided measurement error.
Using the SFM to estimate the model can then be useful in not only recovering consistent estimates of b, but also expected measurement error, u-hat, of each observation. This then means that one can estimate the true value, y*, for each observation as y + u-hat. Wow!
One can think of other examples in economics and other disciplines where a one-sided error term might arise. For instance, Kumbhakar & Parmeter (2009) use the SFM to analyze bargaining models. Specifically, a firm has a maximum wage it is willing to pay a worker (i.e., the worker's productivity). However, if the firm has market power, the actual wage paid may be below the worker's productivity. Thus, the one-sided error captures the deviation between a worker's wage and his/her/their true productivity and reflects the bargaining power of the firm. Double wow!
Stepping back from these specific examples, there are two larger points to emphasize. First, when reading papers ...
Think about what else the components of the model could represent. In my view, this is the easiest way to come up with interesting, new research ideas. I owe this bit of "philosophy" to my advisor and mentor, the wonderful Dr. Mark Pitt. now long since retired.

Post-PhD Defense, Brown U, 1999
One of the few pearls of wisdom I can still recall from him (I'm old and the memory fades) is "Do not reinvent the wheel!" If you can contribute to scientific advancement by borrowing from the work of others, then do it.
Second, the only way to find models in one area that may be useful in a completely re-imagined way in another area is to pay attention outside your area. Read outside your particular niche, attend seminars outside your focus, talk to as many people as you can, follow twitterers from all specializations and disciplines. And, when they describe the trees in their area, you look for the forest!

UPDATE (5.11.20)
Luke Taylor reminded me of his working paper, joint with Shin Kanaya, which I had quickly read before but forget when writing this post. The paper, entitled "Type I and Type II Error Probabilities in the Courtroom," goes beyond the Hausman et al. (1998) approach econometrically, but the spirit is identical to my discussion above. The abstract has a great opening line: "We estimate the likelihood of miscarriages of justice by reframing the problem in the context of misclassified binary choice models." Well done!
References
Aigner, D., C.A. Knox Lovell, and P. Schmidt (1997), "Formulation and Estimation of Stochastic Frontier Production Function Models." Journal of Econometrics, 6, 21–37
Battese, G.E. and T.J. Coelli. (1988). “Prediction of Firm-Level Technical Efficiencies With a Generalized Frontier Production Function and Panel Data,” Journal of Econometrics, 38, 387-399
Hausman, J.A., J. Abrevaya, and F.M. Scott-Morton (1998), "Misclassification of the Dependent Variable in a Discrete-Response Setting," Journal of Econometrics, 87(2), 239-269
Kumbhakar, S.C. and C.F. Parmeter (2009), "The Effects of Match Uncertainty and Bargaining on Labor Market Outcomes: Evidence From Firm and Worker Specific Estimates," Journal of Productivity Analysis, 31(1), 1-14
Millimet, D.L. and C. Parmeter (2019), "Accounting for Skewed or One-Sided Measurement Error in the Dependent Variable," IZA DP No. 12576
Palangkaraya, A., E. Webster, and P.H. Jensen (2011), "Misclassification Between Patent Offices: Evidence from a Matched Sample of Patent Applications," Review of Economics and Statistics, 93, 1063-1075
Taylor, L. and S. Kanaya (2020), "Type I and Type II Error Probabilities in the Courtroom," unpublished manuscript